从Logistic Regression到FTRL

Logistic Regression在Linear Regression的基础上，使用sigmoid函数将y=θx+b的输出值映射到0到1之间，且log(P(y=1)/P(y=0)) = θx+b。并且在靠近0.5处坡度较大，使两侧快速趋于边界。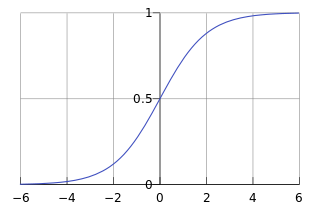

Hypothesis可以认为是y=1时的概率，表示为: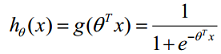


如果使用与线性回归相同的平方损失函数函数，那么是“non-convex”的，不利于求得最优解。因此选择对数似然损失函数(log-likelihood loss function)作为逻辑回归的Cost Function: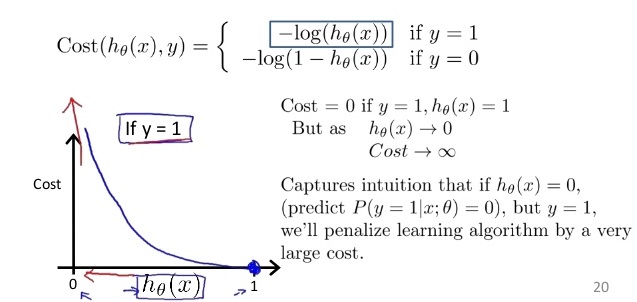

将两式合并可以得到Cost Function（最大似然的负数就是损失函数，最大化似然函数和最小化损失函数是等价的）：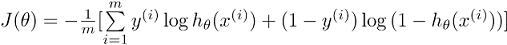

正则化

为控制模型的复杂度，通常在损失函数中加L1或L2范数做正则化（regularization），通过惩罚过大的参数来防止过拟合。L1范数是指向量中各个元素绝对值之和，也称为Lasso regularization；L2范数是指向量中各个元素平方之和, 也称为Ridge Regression。
L1正则化产生稀疏的权值，因此可用来做特征选择，在高维数据中使用更为广泛一些；L2正则化产生平滑的权值（还有一种说法认为L2限制了解的空间，因此可以加速收敛速度，但实际作用并不大）。L1在实际中使用的更多一些，L2和L1要配合使用，增加L2会减弱L1的系数作用。

数学公式解释

  • L1的权值更新公式为wi = wi – η * 1, 权值每次更新都固定减少一个特定的值(学习速率)，那么经过若干次迭代之后，权值就有可能减少到0。
  • L2的权值更新公式为wi = wi – η * wi，虽然权值不断变小，但每次减小的幅度不断降低，所以很快会收敛到较小的值但不为0。

几何空间解释


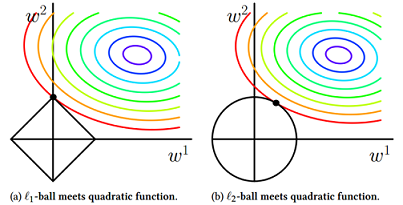
在二维空间中，左边的方形线上是L1中w1/w2取值区间，右边得圆形线上是L2中w1/w2的取值区间，圆圈表示w1/w2取不同值时整个正则化项的值的等高线。从等高线和w1/w2取值区间的交点可以看到，L1中两个权值倾向于一个较大另一个为0，L2中两个权值倾向于均为非零的较小数。

求解方法

Gradient Descent

梯度下降法通过沿着目标函数梯度相反的方向更新参数达到最小化目标函数的目的。梯度下降的最终点并非一定是全局最小点，受初始点的选择影响可能会陷入局部最小点。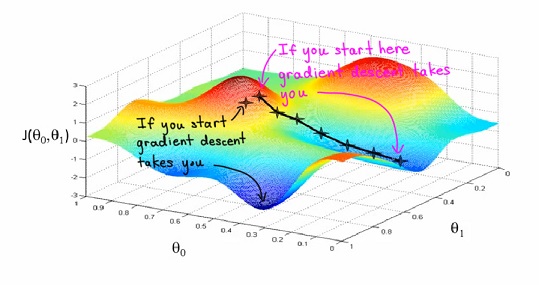

根据g(z)和y=lnx的偏导y'=1/x，对LR的损失函数求偏导，可以得到梯度: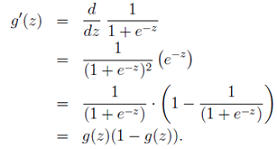

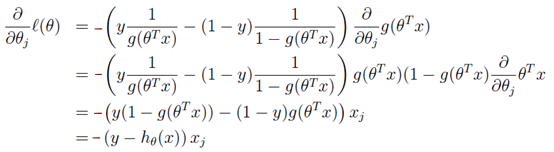
更新时θi会向着全局梯度最小的方向进行减少：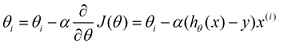

按照每次更新使用的样本量，梯度下降分为批量梯度下降法（Batch Gradient Descent）、随机梯度下降法（Stochastic Gradient Descent）、小批量梯度下降法（Mini-batch Gradient Descent）

Batch Gradient Descent：

更新每一参数时都使用所有的样本来进行更新。

  • 优点：凸函数保证得到全局最优解；易于并行实现。
  • 缺点：大数据更新速度慢，内存无法装下所有数据；无法实时更新

Stochastic Gradient Descent　

利用每个样本的损失函数对θ求偏导得到对应的梯度

  • 优点: 迭代速度快；可用于实时更新
  • 缺点: 目标函数zigzag波动大；不保证得到全局最优解，但是随着更新逐渐缩小步长几乎可以达到与BGD相同的效果；不利于并行实现

Mini-batch Gradient Descent

MBGD在BGD和SGD之间做了取舍，既保证了高效的训练速度，又保证了稳定的收敛，是大数据集下常用的方法。batch的大小一般取50-256之间。

L-BFGS & OWLQN

  1. 梯度下降法是基于目标函数梯度进行搜索，收敛速度是线性的。
  2. 牛顿法同时使用一阶段数和二阶导数（Hessian矩阵）进行搜索，收敛速度快。尤其在最优值附近时，收敛速度是二次的。牛顿法需要计算Hessian矩阵的逆矩阵，当维度过高矩阵稠密时运算和存储量巨大。
  3. 拟牛顿法（Quasi-Newton）用一个近似矩阵来替代逆Hessian矩阵。BFGS是拟牛顿法的一种，使用”Backtracking line search”搜索步长，使用”two loop recursion”更新参数。
  4. BFGS虽然不需要计算Hessian矩阵了，但是保存历史记录仍需要消耗大量的内存。L-BFGS，即限定内存的BFGS算法，由最近的m次输入变量和梯度变量的差值近似更新矩阵。
  5. OWLQN(Orthant-Wise Limited-memory Quasi-Newton)是在L-BFGS基础上解决L1-norm不可微提出的，每次迭代都不改变参数的正负性，使得正则项变成可微的。对于需要变换符号的参数，将其置为0，通过在下次迭代中选择合适的象限来改变参数的正负。

Online Learning

使用流式样本进行模型的实时训练时，OGD(online gradient descent)不能非常高效的产生稀疏解，常见的做稀疏解的途径:

  • 简单截断：设定一个阈值，每online训练K个数据截断一次。无法确定特征确实稀疏还是只是刚刚开始更新。
  • 梯度截断(Truncated Gradient): 当t/k不是整数时，采用标准的SGD,当t/k是整数时，采取截断技术。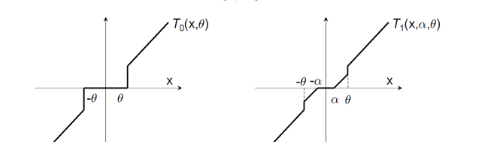
  • FOBOS(Forward-Backward Splitting)：由标准的梯度下降和对梯度下降的结果进行微调两部分组成，确保微调发生在梯度下降结果的附近并产生稀疏性。FOBOS可以看做TG在特定条件下的特殊形式随着的增加，截断阈值会随着t的增加逐渐降低。
  • RDA(Regularized Dual Averaging): 是一种非梯度下降类方法，判定对象是梯度的累加均值，避免了由于某些维度由于训练不足导致截断的问题；RDA的“截断阈值”是常数，截断判定上更加aggressive，更容易产生稀疏性，但会损失一些精度。

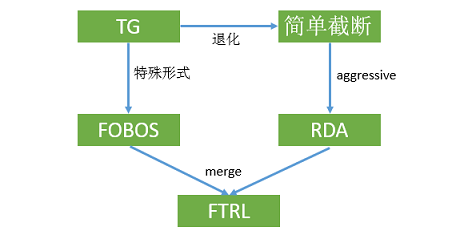
FTRL(Followed the Regularized Leader)

FTRL综合考虑了FOBOS和RDA的优点，兼具FOBOS的精确性和RDA优良的稀疏性，Google 2013年发布在KDD的《Ad Click Prediction: a View from the Trenches》给出了详细的工程实践。

思想及实现

特征权重更新公式为: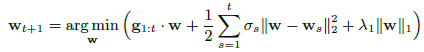

第一部分为累计梯度和，代表损失函数下降的方向；第二部分表示新的结果不要偏离已有结果太远；第三部分是正则项，用于产生稀疏解。将第二项展开可以表示为：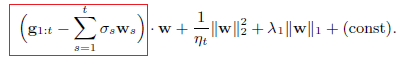

因此只需要保存第一部分的累加和，并在每轮更新前都进行累计就可以完成权重的更新。更新算法如下：

Per-Coordinate根据每个特征在样本中出现的次数来推算它的学习率。如果出现的次数多，那么模型在该特征上学到的参数就已经比较可信了，所以学习率可以不用那么高；而对于出现次数少的特征，认为在这个特征上的参数还没有学完全，所以要保持较高的学习率来使之尽快适应新的数据。

Memory Saving策略

  • Probabilistic Feature Inclusion：丢弃训练数据中很少出现的特征。离线训练可以通过预处理过滤，这里给出了两个在线训练的方法：
    • Poisson Inclusion：当一个新特征出现时，以固定概率P接受并更新
    • Bloom Filter Inclusion：用布隆过滤器记录某个特征是否出现了n次，同样也是基于概率的，因为布隆过滤器有一定的概率误判
  • Encoding Values with Fewer Bits：由于需要保存的数据一般处于[-2,2]之间所以使用64位浮点数存储浪费了空间。使用q2.13编码保存，即小数点前寸2位小数点后寸13位正负号寸一位。这样可以节省75%的内存，并且准确度基本没有损失。
  • Training Many Similar Models：当需要训练多个模型的变种时，每个模型都单独训练会浪费很多资源；如果把一个固定的模型作为先验学习残差，无法处理移除或替换特征的情况。经过观察发现：每一维的特征都跟特定的数据有关，每个模型的变种都有自己独特的数据。因而，可以用一张hash表来存储所有变种的模型参数，以及该特征是哪个变种模型。
  • A single Value Structure：当模型需要增加或者减少一批特征时，此时共享的特征只保留一份，用一个位数组来记录某个特征被哪些模型变种共享。对于一个样本，计算所有模型的更新值并取平均值更新共享参数。
  • Computing Learning Rates with Counts：使用正负样本的比例来近似计算梯度的和。
  • Subsampling Training Data：负样本按r的概率采样在训练时乘一个1/r的权重来弥补负样本的缺失。

参考