为了赶上1月开课的Game Theory II: Advanced Applications,最近补习了前序课。本课程主要讲了博弈论中的基础问题和概念,除了对slides做了一些摘要外,还结合了其他资料及自己的心得进行了注释,在后续学习过程中会不断添加延伸资料(如知乎上的相关讨论)。
The course covers the basics: representing games and strategies, the extensive form (which computer scientists call game trees), repeated and stochastic games, coalitional games, and Bayesian games (modeling things like auctions). This note includes following sections:
1: Introduction and Overview
2: Mixed-Strategy Nash Equilibrium
3: Alternate Solution Concepts
4: Extensive-Form Games
1: Introduction and Overview
1.1 Nash Equilibrium
1.1.1 Presumption
- A consistent list of actions
- Each player’s action maximizes his or her payoff given the actions of the others
- A self-consistent or stable profile
1.1.2 E.g. Keynes Beauty Contest Game: The Stylized Version
- Each player names an integer between 1 and 100
- The player who names the integer closest to two thirds of the average integer wins a prize, the other players get nothing
- Ties are broken uniformly at random
1.1.3 Summary
- Each player’s action maximizes his or her payoff given the actions of the others
- Someone has an incentive to deviate from a profile of actions that do not form an equilibrium (第1次参与游戏时: Median 33, Winner 23)
- Nobody has an incentive to deviate from their action if an equilibrium profile is played (第2次参与游戏时: Median 2, Winner 4)
1.1.4 Definition
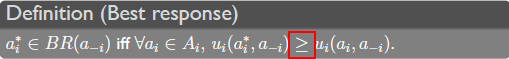
玩家在当前局面的收益最大化的选择
纳什均衡是这样的一种状态:在博弈中如果玩家A选择了X选项,那么玩家B为了使自己的利益最大话选择了Y选项;相反如果玩家B选择了Y选项,这种情况下X对于玩家A来说也是利益最大话的唯一选项
1.1.5 Example Games
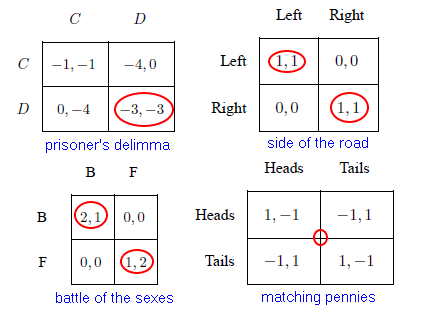
1.2 Domination
- If one strategy dominates all others, we say it is dominant
- A strategy profile consisting of dominant strategies for every player must be a Nash equilibrium
- An equilibrium in strictly dominant strategies must be unique
1.3 Pareto Optimality
- when an output is at least good for everyone as another and strictly preferred by someone, we say the it Pareto-dominates another
- an output is Pareto-optimal if there is no other outcome that Pareto-dominates it
- a game can have more than one Pareto-optimal outcome
- every game have at least one Pareto-optimal outcome
- The paradox of Prisoner’s dilemma: the (DS) Nash equilibrium is the only none-Pareto-optimal outcome!
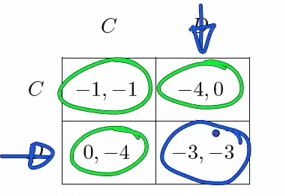
“从此以后,非损人不能利己。” 摘自知乎:如何通俗地解释「帕累托最优」(Pareto optimum)?
介绍Dominant Strategy Equilibrium的视频1.3.1 Braess’ paradox(布雷斯悖论)
有4000辆车从START到达END,如果只开通实线表示的路,在纳什均衡的条件下,各有2000辆车分别通过A和B,每辆车花费65分钟。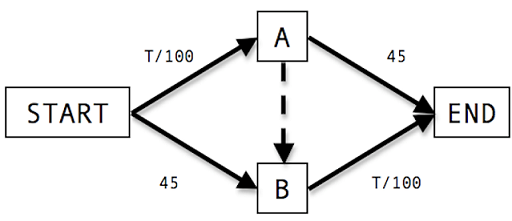
当增加虚线代表的路后,由于T/100<45,所有的司机都倾向于START-A-B-END的路线。但对于所有司机而言,花费的时间变为80分钟。
新加的路增加了一个更加低效的纳什均衡点,Nash Equilibrium不总是全局最优解。由于每个人都是自私的而不是相互协作的,每一个个体都企求扩大自身可使用的资源,然而资源耗损的代价却转嫁所有可使用资源的人们。这种个人利益与公共利益对资源分配有所冲突的社会陷阱成为“公地悲剧”(Tragedy of the Commons)
2: Mixed-Strategy Nash Equilibrium
- Pure Strategy:每个选手只选定一种策略
- Mixed Strategy: 每个选手的策略选择都是多个Pure Strategy的概率分布
Theorem (Nash, 1950): Every finite game has a Nash equilibrium.
2.1 Computing
纳什均衡,就是要使得别人在自己的概率下没法区别他的策略,否则对手会选择对自己更有利的策略
类似的,可以计算出选手1的概率分布(2/3,1/3)
然而,当维度增加时,纳什均衡的求解是NP完全的
3: Alternate Solution Concepts
3.1 Iterated Removal
通过移除Dominated Strategies来简化/求解纳什均衡
3.1.1 Strictly Dominated Strategies:
- preserves Nash equilibrium
- It can be used as a preprocessing step before computing an equilibrium
- order of removal doesn’t matter
3.1.2 Weakly Dominated Strategies:
- At least one equilibrium preserved.
- Order of removal can matter.
3.2 Maxmin Strategies

在其他玩家选择对其伤害最大的策略时,自己的最小收益最大化
Why would I want to play a maxmin strategy?
- a conservative agent maximizing worst-case payoff
- a paranoid agent who believes everyone is out to get him

Why would I want to play a minmax strategy? - to punish the other agent as much as possible
Theorem (Minimax theorem (von Neumann, 1928): In any finite, two-player, zero-sum game, in any Nash equilibrium each player receives a payoff that is equal to both his maxmin value and his minmax value.
- Each player’s maxmin value is equal to his minmax value. The maxmin value for player 1 is called the value of the game
- For both players, the set of maxmin strategies coincides with the set of minmax strategies
- Any maxmin strategy profile (or, equivalently, minmax strategy profile) is a Nash equilibrium. Furthermore, these are all the Nash Equilibria. Consequently, all Nash equilibria have the same payoff vector
4.Extensive-Form Games
用树形结构表示多位player的交替行为及收益

Theorem: Every perfect information game in extensive form has a PSNE
This is easy to see, since the players move sequentially
一颗子树是一个Subgame。Subgame均衡的纳什均衡才可信(与Subgame不均衡的相比往往是在其他走不到的子树上有区别)。据此可以从叶节点倒推出均衡状况。
4.1 Subgame Perfect Equilibrium
- Definition:策略S对于所有的子图来说,都是Nash Equilibrium,则S称为subgame perfect equilibrium
- Computing:Backward Induction, maxmin Algorithm, alpha-beta pruning
- Application:Centipede Game
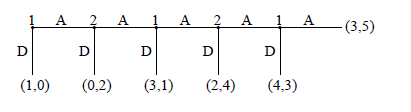
知乎:蜈蚣博弈(Centipede Game)在现实中都有哪些应用?
4.2 Imperfect information Extensive-Form Games
有了等价结点的概念,Player只能知道目前在某一类等价节点,无法区分具体位置
