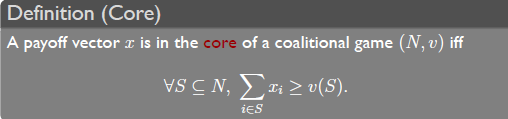The course covers the basics: representing games and strategies, the extensive form (which computer scientists call game trees), repeated and stochastic games, coalitional games, and Bayesian games (modeling things like auctions). This note includes following sections:
5: Repeated Games
6: Bayesian Games
7: Coalitional Games
5: Repeated Gmaes
5.1 Utility
可以定义为均值的极限,也可以定义为指数加权和的极限
对衰减系数的两种解释:
- 选手更在意近期的收益而非长期收益
- 在每一轮中,游戏都有
1-β^i的概率结束
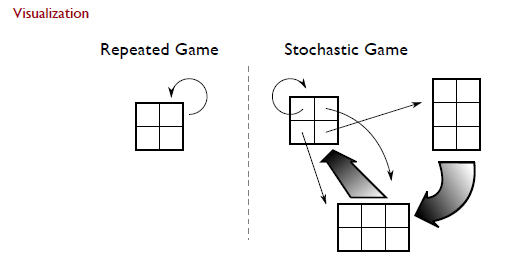
5.2 Stochastic Games
Stochastic Games是Repeated Gmaes的泛化形式,agents可以重复参与一组normal-form games,下一轮选择的game取决于上一个game及所有agent的actions
it also generalizes MDP (Markov Decision Process), MDP is a single-agent stochastic game.
5.3 Learning in Repeated Games
5.3.1. Fictitious Play
观察对手前面行为的分布,选择频率最大的一个作为对手下一轮的assessed strategy,并作出最佳回应(pure strategy)
Theorem:If the empirical distribution of each player’s strategies converges in fictitious play, then it converges to a Nash equilibrium.
5.3.2. No-regret Learning
不取决于对手建模,只关注自己的经验。
t时刻没有采用策略s的regret值=采用的s的utility-真实的utility。
按照不同策略的regret值分布选择t+1时刻的策略。
5.4 Equilibria
5.4.1 Some famous strategies (repeated PD):
- Tit-for-tat: Start out cooperating. If the opponent defected, defect in the next round. Then go back to cooperation
- Trigger: Start out cooperating. If the opponent ever defects, defect forever.
5.4.2 Nash Equilibria
- 如果任何player的payoff都不小于他的minmax value(当其他player都执行minmax策略时的收益),则这个playoff profile是enforceable的
- 如果存在一个合理、非负、和为1的概率分布,使得集合中每个playoff都能表示为不同策略utility的加权和,则这个playoff profile是feasible的
Folk Theorem (Part 1):Payoff in Nash → enforceable
Folk Theorem (Part 2):Feasible and enforceable → Nash
5.5 Discounted Repeated Games
将utility定义为时间衰减的指数加权
Repeatedly playing a Nash equilibrium of the stage game is always a subgame perfect equilibrium of the repeated game
6: Bayesian Games
- a set of games that differ only in their payoffs, a common prior defined over them, and a partition structure over the games for each agent. 一组游戏,相同的策略空间,不同的utility。
- Directly represent uncertainty over utility function using the notion of epistemic type
Bayesian (Nash) Equilibrium: 在对手的action和type分布上最大化自己的expected utility.
- strategic uncertainty about how others will play
- payoff uncertainty about the value to their actions
7: Coalitional Games
agent之间相互cooperative,关注集体的payoff,playoff在团体内重新分配。
7.1 The Shapley Value
Lloyd Shapley’s idea: members should receive payments or shares proportional to their marginal contributions。根据边际收益分配利益,需要遵循如下3个公理确保分配的公平性:
- Symmetry: i and j are interchangeable relative to v if they always contribute the same amount to every coalition of the other agents. Interchangeable agents should receive the same shares/payments.
- Dummy player: i is a dummy player if the amount that i contributes to any coalition is 0. Dummy players should receive nothing.
- Additivity: If we can separate a game into two parts v = v1 + v2, then we should be able to decompose the payments
Theorem: 当满足Symmetry, Dummy player and Additivity 三个公理时,每一个Coalitional Games都有唯一一组payoff分配方案
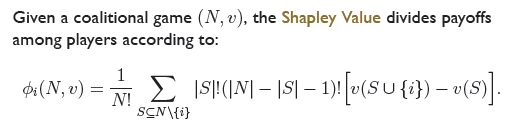
7.2 The Core
Shapley Value保证了fairness缺忽略了stability. 有时更小的coalition虽然整体收益较小但却更有吸引力,因此个体不愿意组成grand coalition。
每个个体在集体中得到的都要大于等于个体可以独自获得的payoff。类似于Nash Equilibrium。