This advanced course considers how to design interactions between agents in order to achieve good social outcomes. Three main topics are covered:
1:Social Choice theory(i.e., voting rules)
2:Mechanism Design
3:Efficient Mechanisms(VCG)
4:Auctions
1.Social Choice
1.1 Voting Schemes
- Plurality:选择每个agent最喜欢的候选计数。
- Plurality with elimination:如果某一个候选占据了大多数则结束,否则淘汰得票最低的进行下一轮投票。
- Borda Rule, Borda Count:每个agent的preference ordering记0~n-1分,计算每个候选人的总得分。
- Successive elimination:每一轮两个候选人pk,获胜者与下一个候选人继续pk。pk的顺序影响最终结果
- Condorcet Consistency:如果一个候选在起其他所有候选的pairwise比较中胜出则被选中,有时会形成Condorcet Cycle
1.2 Paradoxical Outcomes

1.2.1 Impossibility of Non-Paradoxical Social Welfare Functions
w:将所有agent的preference order变为一个order的函数(social welfare function)
Wis Pareto efficient(PE) if whenever all agents agree on the ordering of two outcomes, the social welfare function selects that ordering.Wis independent of irrelevant alternatives(IIA) if the selected ordering between two outcomes depends only on the relative orderings they are given by the agents.Whas a dictator if there exists a single agent whose preferences always determine the social ordering.Theorem (Arrow, 1951): Any social welfare function W over three or more outcomes that is Pareto efficient and independent of irrelevant alternatives is dictatorial.
1,2直觉上与3相矛盾,却相生相依,通常牺牲IIA解决悖论
1.2.2 Impossibility of Non-paradoxical Social Choice Functions
C:根据所有agent的preference order选出部分候选集(social choice functions)
- weakly Pareto efficient:A dominated outcome can’t be chosen
- monotoni:an outcome o must remain the winner whenever the support for it is increased in a preference profile under which o was already winning
- dictatorial:
Calways selects the top choice in j’s preference ordering.Theorem (Muller-Satterthwaite, 1977):Any social choice function that is weakly Pareto efficient and monotonic is dictatorial.
2.Mechanism Design(机制设计)
对于一组Bayesian game setting(机制设计者不可能改变的因素),Mechanism是agent的行为集合及行为到profile分布的映射。每个agent都保守着自己的信息,机制不能改变agent的偏好和type的空间。
机制设计通过提供一个关注激励社会成员汇报自己私有信息问题的分析框架,研究如何设计一个博弈形式,令社会成员参与其中,得出的博弈解恰好符合设计者所想达到的社会选择。
Dominant Strategies Implementation:在dominant strategies上得到均衡点,使得每个均衡点的profile等于social choice functions的机制。
Bayes–Nash Implementation:在信息不完整的game中存在一个Bayes–Nash equilibrium,使得每种行为的profile等于每个type的social choice functions
2.1 Revelation Principle
any social choice function that can be implemented by any mechanism can be implemented by a truthful, direct mechanism
“The agents do not have to lie, because the mechanism already lies for them.”
2.2 Impossibility of General, Dominant-Strategy Implementation
让所有的agent都享有dominant Strategy是不可行的,可通过如下方式化解Gibbard–Satterthwaite theorem:
- 使用限制更弱的implement,比如Bayes–Nash implementation
- 规定agent不能随意选择任意的preference
2.3 Transferable Utility
假如一个type的agent的收益函数=原始的utility-agent的payment(两者互不影响),那么称这个agent具有quasilinear preferences with transferable utility。因此机制设计拆解为社会结果选择函数(choice rule)与实体支付函数(payment rule)两部分。
transferrable utility mechanism考虑的因素:
- Truthfulness(strategy-proof):direct的,而且每个agent宣称的valuation function(一个agent为了一个选择x愿意付出的最大的代价的映射)都是真实的。
- Efficiency:忽视monetary payments,最大化所有agent收益的总和,则这个transferrable utility mechanism是strictly Pareto efficient, or just efficient。(social-welfare maximization)
- Budget balance:所有agent的payment和等于0
- Individual-Rationality:参与机制的收益期望大于等于0(ex-interim) / 一定大于0(ex-post)
- Revenue Maximization/Minimization: payment总额最大 / 最小化
- Maxmin fairness: make the least-happy agent the happiest,让收益最低的情况的收益额尽可能高.
- Price of Anarchy Minimization:Minimize the worst-case ratio between optimal social welfare and the social welfare achieved by the given mechanism(无限趋近efficiency)
3. Efficient Mechanism(VCG)
3.1 The Vickrey-Clarke-Groves Mechanism
Groves机制的概念与Clarke机制相比更广。在对货币的效用函数拟线性的假设下,Groves机制是strategy proof,也就是鼓励人说真话,同时也是Pareto optimal。Clarke机制要求进入的消费者用税的形式支付自己的进入而带来的公共物品的变化从而导致的其他消费者总效用的损失。Vickrey拍卖是Clarke机制在拍卖中的具体应用.。
Definition: 选择总收益最大的一组输出,每个agent的payment=当你参与时其他人的utility的总和 - 当你不参与时其他人的utility的总和,则这个Groves mechanism称为VCG(或pivotal mechanism)。
you get charged everyone’s utility in the world where you don’t participate(social cost)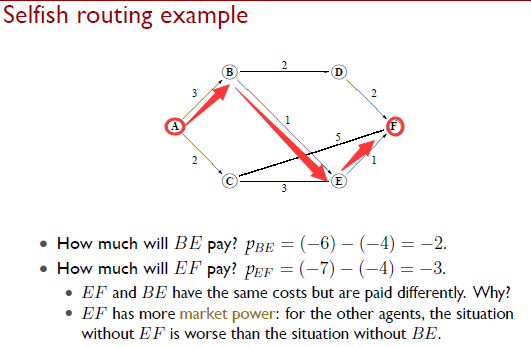
Theorem: Truth telling is a dominant strategy under any Groves mechanism including the pivotal mechanism (a VCG mechanism).
Theorem (Green–Laffont): an “efficient” mechanismhas truthful reporting as a dominant strategy for all agents and preferences only if it is Groves mechanism.
3.2 Limitations of VCG
- Privacy: private information may have value to agents that extends beyond the current interaction
- Susceptibility to Collusion: 多人密谋谎报utility可以在不影响结果的情况下减少total payment
- not Frugal: VCG can end up paying arbitrarily more than an agent is willing to accept
- Revenue Monotonicity Violated: revenue always weakly increases as agents are added
- Cannot Return All Revenue to Agents(一些非盈利的机制)
3.3 Effiency、Individual Rationality and Budget Balance in VCG
- Choice-set monotonicity:移除某个agent不会增加机制的候选集
- No negative externalities:every agent has zero or positive utility for any choice that can be made without his participation
Theorem: The VCG mechanism is ex-post individual rational when the choice set monotonicity and no negative externalities properties hold.
- No single-agent effect: 移除了某个agent,其他agent的welfare总和不会减少
Theorem: The VCG mechanism is weakly budget-balanced when the no single-agent effect property holds.
有时想要设计出一个Efficient的机制是不可能的,需要在incentives和efficiency之间做让步
Theorem (Myerson–Satterthwaite): There exist distributions on the buyer’s and seller’s valuations such that: There does not exist any Bayesian incentive-compatible mechanism that is simultaneously efficient, weakly budget balanced and interim individual rational.
Example:Proof for fully budget balanced trade that is ex-post individually rational.
4.Auctions
4.1 Some Canonical Auctions
- English Auction: 从reservation price开始bidder相继抬价直到没有更高的出价
- Japanese Auction: 类似于English,但由auctioneer出价,bidder回应,避免价格大范围跳动
- English and Japanese auctions are extensive form games
- Theorem:Under the independent private values model (IPV), it is a dominant strategy for bidders to bid up to (and not beyond) their valuations in both Japanese and English auctions.
- Dutch Auction:从高价开始价格逐渐降低,直到有人响应
- First-Price Auction:bidder同时出价,出价最高的已最高价获得所有权
- First-Price (sealed bid) and Dutch auctions are strategically equivalent
- Theorem: In a first-price auction with two risk-neutral bidders whose valuations are IID and drawn from U(0,1), (v1*1/2,v2*1/2) is a Bayes-Nash equilibrium strategy profile.
- Theorem: In a first-price sealed bid auction with n risk-neutral agents whose valuations are independently drawn from a uniform distribution on [0,1], the (unique) symmetric equilibrium is given by the strategy profile(vi*(n-1)/n).
- Second-Price Auction:bidder同时出价,出价最高的以第二高价获得所有权
- Second-Price Auction is special form of VCG
- Theorem: Truth-telling is a (weak) dominant strategy in a second-price auction
4.2 Revenue Equivalence
Revenue Equivalence Theorem: Assume that each of n risk-neutral agents has an independent private valuation for a single good at auction, each drawn from cumulative distribution F. Then any two auction mechanisms in which
(1)in equilibrium, the good is always allocated in the same way; and
(2)any agent with valuation 0 has an expected utility of 0;
both yield the same expected revenue, and both result in any bidder with valuation v making the same expected payment.
RET是Auction Theory中最重要的Theorem,Paul Klemperer的Why Every Economist Should Learn Some Auction Theory第一章有关于RET的解释和举例。
4.3 Optimal Auctions
最大化卖家收入,可以通过牺牲efficiency设置reserve price来实现(前提是individual rational/risk-neutral和分布已知)
上面是累积分布函数,下面是概率密度函数。如果他是单调增长的, 最好的reserve price就是V.V.=0的时候.
Myerson Theorem:Single-good下,direct机制里,Optimal Auction即把东西卖给V.V.最大的人,且V.V.最大的人支付第二高V.V.


