Top-k推荐是实际推荐场景下常用的推荐模式,由于为用户展示的Item数量有限,因此推荐更关注列表顶部结果的指标。Learning to Rank技术在实际推荐应用中起到了非常重要的作用,排序算法按照建模方式分为Pointwise、Pairwise和Listwise三种。
1.Pointwise
1.1 Matrix Factorization
由Koren在Nexflix比赛期间提出并大获成功,将user对Item的偏好看做评分矩阵(稀疏矩阵),通过SGD等方法将矩阵分解为两个低维度矩阵P(|U|*K)和Q(|I|*K),用latent factor分别代表User和Item的属性,对应向量的叉乘获取预测评分。在损失函数中增加正则项和bias项可显著提高效果。扩展算法在建模过程中考虑了更多因素,如SVD++、TimeSVD、TrustSVD等。
1.2 Factorization Machines
FM可以看做是MF的generalized版本,不仅能够利用普通的用户反馈信息,还能融合情景信息、社交信息等诸多影响个性化推荐的因素。与传统的非线性模型相比,降低了参数维度,作为特征预处理和预测算法被广泛应用于广告、推荐、搜索等业务。
假如忽略任何额外信息,那么一条评分数据对应的特征就只涉及到一个用户id,一个物品id,将前三项分别看成全局、用户、物品的bias,最后一项刚好是两个隐因子向量的内积,等同于带bias的SVD模型。
主要参数
- k: 控制交叉项的复杂度,k值增大可以逼近任意复杂的二次交叉特征, 但是也会造成过度拟合.
- lamda:在特征集较大时,k值的引入很容易导致过拟合现象,但是模型本身规定了特征交叉的形式,因此在FM模型中,不能像线性模型中一样通过减少特定的特征组合来减弱过拟合。而是通过引入L2正则项来约束过拟合。
- n:迭代轮数。迭代次数可以使得数据训练的相对充分,但是在数据集较大的情况下其性能上的优化并不大,因为在一轮迭代过程中特征训练的已经相对充分了
- Learning_rate: 学习速率太大会导致模型权重震荡,太小则需要较长的迭代时间。实际中一般使learning rate随着迭代次数不断衰减。
与其他模型的比较
通过将特征的交叉映射到低纬度的空间,在特征交叉的同时达到了特征降维的效果,兼具了SVM等模型的非线性特征和latent factor model适用于稀疏数据的特征。形式上与一般的线性回归相似,特殊的地方是对组合特征的处理,在稀疏特征环境下,这种对组合特征的处理使得该模型更适合做推荐。
1.3 OrdRec
Korend大神提出,2011 RecSys best paper。将用户对物品的评分用1…S共S个等级而不是具体的数值来表示,相邻两个等级之间的差用β表示,因此模型的参数就是t1及S-2个β。根据训练集中的评分等级训练评分的概率分布,通过每一个评分等级与其相邻的阈值之差构造误差函数 P(r=t|β)=P(r<=t|β)-P(r<=t-1|β),用随机梯度下降算法对阈值参数求解threshold,得到评分等级整体的概率分布情况。
1.4 Restricted Boltzmann Machines
RBM对二分类的偏好数据进行latent factor分析,本质上是一个随机神经网络(节点的状态取决于相连节点的状态),每个visible unit连接所有的hidden unit和bias unit,同时bias unit还有所有hidden unit相连。算法参数是连接visible unit和hidden unit的无向边的权重Wij,不同用户使用不同的hidden unit和hidden unit状态,但是共享一组weight。详见论文Restricted Boltzmann Machines for Collaborative Filtering,或者这个introduction.
1.5 Sparse LInear Methods
SLIM: Sparse Linear Methods for Top-N Recommender Systems
2.Pairwise
2.1 EigenRank
发表于08年SIGIR,提出了ranking-oriented CF的架构,并给出了贪心法和随机游走两种简单的算法实现。详见论文EigenRank: A Ranking-Oriented Approach to Collaborative Filtering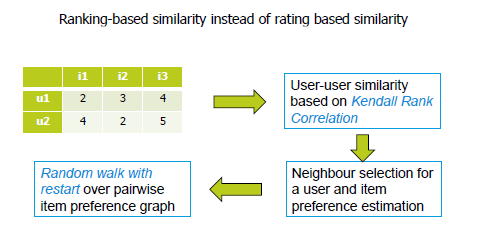
Kendall Rank Correlation Coefficient
在rating-based相似度计算中,根据user对item的打分计算u2u相似度及i2i相似度;在ranking-oriented方案中,根据user对item的偏好关系(关注打分的顺序而非数值)计算相似度,KRCC取决于两者序列中不对称pair的数量,即在一个序列中i排序高于j而在另外一个序列中i低于j。
Greedy Order Algorithm
- 根据neighborhood-based CF构造user对item的偏好关系(投票表决i和j的相对位置),这个偏好关系是没有传递性的。
- 计算每个item初始的potential分:the more items that are less preferred than i, the higher the potential of i.
- 每次选取potential分数最高的item并更新其他item的potential分(移除当前item对其它item的影响):π(i)+=p(t,i)-p(i,t)
Random Walk Model
用Markov chain model做item排序,状态表示item,偏好函数(依然用neighborhood-based CF构造)表示转移概率。
Comments
- 较早提出了ranking-oriented CF的路子,idea值得称赞,内容比较糙
- 对照组选取有问题,为什么不选用效果更好的item-based CF而选用user-based CF作为baseline?与model-based CF相比效果如何?
- 如何证明Preference Functions没有传递性,如果有传递性,Greedy算法的更新策略就有点问题了。
2.2 Bayesian Personalized Ranking
Rendle在2009年提出,在一个base算法基础之上通过反馈数据构造偏序对,直接对偏序对预测值大小关系构造损失函数优化base算法参数。详见论文BPR: Bayesian Personalized Ranking from Implicit Feedback
Sampling
如果使用full gradient descent,数据倾斜导致收敛速度慢;每次迭代梯度变化过大不易正则化。如果使用stochastic gradient decent,同一个user-item会有连续的多次更新。因此采用可替换的bootstrap sampling。
但是当商品流行度分布不均匀时(tailed distribution),随机选取(c,i)是i很可能是一个流行度很高的item,因此y(c,i)-y(c,j)趋于0,模型更新获得了很小的梯度导致更新效率低。
Improving Pairwise Learning for Item Recommendation from Implicit Feedback提出了一种全新的采样方式:每次选取负样本时倾向于rank较高的item,且采样函数会随模型参数的变化而变化。这种非均匀的采样方式可以大幅提高收敛速度并小幅提高效果,由于采样函数复杂度增加,算法整体的复杂度变化不大。
适用场景
- 理论上pairwise的效果好于pointwise,但由于实现代价较高,使用并不多
- 可用于多目标学习,例如要同时优化CTR、CVR、加购率等指标,在构造样本时可假设:购买>加购>点击>未点击
- 当特征较多而样本不足时,pairwise的方式可提供更多的样本
3.Listwise
3.1 CoFiRank
将排序问题转化为结构化的预估问题,学习函数最大化排序指标NDCG,详见论文COFIRANK: Maximum Margin Matrix Factorization for Collaborative Ranking
3.2 CLiMF
通过优化Reciprocal Rank损失函数的lower bound优化整个列表的排序。 详见论文CLiMF: Learning to Maximize Reciprocal Rank with Collaborative Less-is-More Filtering
Smooth Reciprocal Rank
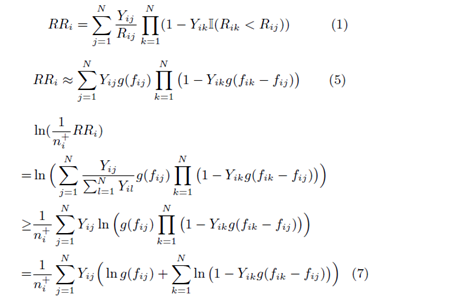
- 通过对(1)中RR的定义看见,RR is a non-smooth function over the model parameters,因此无法使用传统的优化算法直接优化。
- 使用模型预测得分的logistic function代替Rij,得到了(5)的近似表示。
- 根据Jensen’s inequality和Concavity of log function推导出ln(1/n*RR)的lower bound,如(7).可以看出:The maximization of the first term contributes to learning latent factors that promote relevant items, e.g., item j; maximizing the second term turns to learning latent factors of all the other items (e.g., item k) in order to degrade their relevance scores. In sum, the two effects come together to promote and scatter the relevant items at the same time
- 将f(ij)=Ui*Vj带入,就可以使用梯度下降这种标准的优化方法求解UV了
与其他模型对比
- CoFiRank通过优化NDCG损失函数的convex upper bound优化整个列表的排序,适用于评分类的训练数据,;CLiMF适合于二分类的训练数据
- CCF(Collaborative competitive Filtering)考虑了候选集中所有pair的关系(需要构造负样本),CLiMF只考虑相关的pair
- BPR与CLiMF都是直接优化评估指标的smoothed version,但需要负样本;BPR目标是提升所有相关item的排名,而CLiMF目标是提高top-k中相关item的排名
参考
RecSys2013: LTR Tutorial
LibRec: A Java Library for Recommender Systems
Winning the Netflix Prize: A Summary
概述搜索排序算法的评价指标MAP,NDCG,MRR



